Penggunaan Konsep Turunan dalam Menggambar Kurva Polinom
Grafik fungsi merupakan gambaran geometri dari sebuah fungsi. Adanya grafik ini, memudahkan dalam menganalisis nilai fungsi, jenis fungsi, dan sebagainya. Untuk fungsi polinom berderajat 1 (fungsi linear) dan fungsi polinom berderajat 2 (fungsi kuadrat), cara menggambarnya tidak terlalu rumit, bisa hanya dengan beberapa langkah. Tetapi untuk menggambar fungsi polinom berderajat lebih dari 2, membutuhkan bantuan konsep turunan.
Konsep turunan yang dipakai dalam membantu menggambar fungsi polinom ini adalah mengenai fungsi naik, fungsi turun, titik ekstrim, dan jenis ekstrim. Berikut ini selengkapnya pembahasan mengenai langkah-langkah menggambar grafik fungsi dengan bantuan konsep turunan.
Langkah 1: Cari titik-titik penting berupa titik potong terhadap sumbu X, titik potong terhadap sumbu Y, titik ekstrim, dan jenis titik ekstrimnya.
- Titik potong grafik dengan sumbu-sumbu koordinat.
- Titik potong dengan sumbu X didapat jika y = 0.
- Titik potong dengan sumbu Y didapat jika x = 0.
- Cari turunan pertama dan turunan kedua dari fungsi f, yaitu f'(x) dan f"(x).
Dari turunan pertama dapat diperoleh:- interval fungsi naik dan fungsi turun,
- titik ekstrim fungsi f.
- interval fungsi cekung ke atas dan fungsi cekung ke bawah,
- titik belok fungsi.
Langkah 2, Gambarkan titik-titik yang didapat dari langkah 1 pada koordinat kartesius.
Langkah 3, Hubungkan titik-titik yang sudah digambar di koordinat kartesius dengan kurva halus dengan memperhatikan kapan kurva naik dan turun, kapan cekung ke atas, dan kapan kurva cekung ke bawah.
Contoh Soal
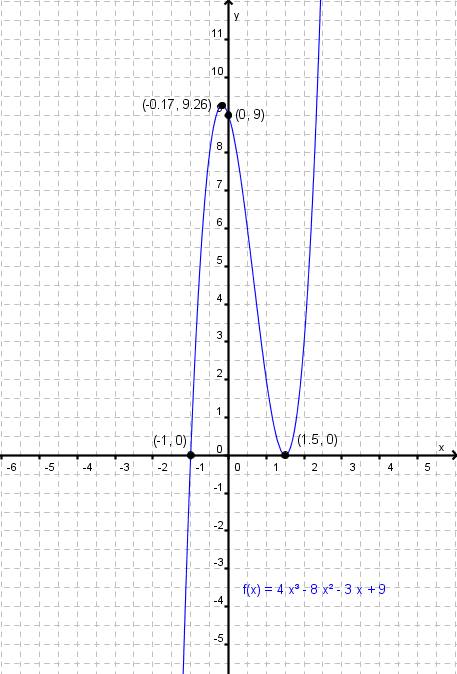
Gambarlah sketsa kurva y=f(x)=4x3-8x2-3x+9.
Jawaban
Untuk menyelesaikannya, mari kita gunakan langkah-langkah yang telah dibahas di atas.
Langkah 1
Titik potong dengan sumbu Y, didapat jika x = 0. y=f(0)=4(0)3-8(0)2-3(0)+9=9 Titik potongnya (0,9)
Titik potong dengan sumbu X, didapat jika y = 0.
Berarti, 4x3-8x2-3x+9=0.
Untuk mendapatkan nilai x, gunakan teorema faktor yang telah dipelajari pada pokok bahasan polinom/suku banyak. Akan didapat x = -1 atau x = 1,5.
Cari turunan pertama dan kedua.
f'(x)=12x2-16x-3
f''(x)=24x-16
Fungsi naik, fungsi turun, dan titik ekstrim.
Fungsi f naik jika f'(x) > 0
12x2 - 16x - 3 > 0
(2x-3)(6x+1) > 0
x < -1/6 atau x > 1,5
Fungsi f turun jika f'(x) < 0
12x2 - 16x - 3 < 0
(2x-3)(6x+1) < 0
-1/6 < x < 1,5
Titik ekstrim diperoleh jika f'(x) = 0
12x2 - 16x - 3 = 0
(2x-3)(6x+1) = 0
x = -1/6 atau x = 1,5
x = -1/6 dalam bentuk desimal bisa ditulis sebagai x = -0,17
Jenis stasioner dapat diperoleh dengan substitusi x ketika f'(x) = 0 ke f"(x).
f"(-1/6) = 24(-1/6) - 16 = -20 < 0
menurut uji turunan kedua, x = -1/6 mempunyai nilai balik maksimum. Nilai balik maksimumnya diperoleh dengan substitusi nilai x ke fungsi awal
f(-1/6) = 9 7/27 = 9,26
f"(1,5) = 24(1,5) - 16 = 20 > 0
menurut uji turunan kedua, x = 1,5 mempunya nilai balik minimum. Nilai balik minimumnya diperoleh dengan substitusi nilai x ke fungsi awal
f(1,5) = 0
Kecekungan fungsi dan titik belok fungsi.
Fungsi f cekung ke atas jika f"(x) > 0
24x - 16 > 0
24x > 16
x > 2/3
Fungsi f cekung ke bawah jika f"(x) < 0
24x - 16 < 0
24x < 16
x < 2/3
Titik belok fungsi f diperoleh jika f"(x) = 0
24x - 16 = 0
24x = 16
x = 2/3
f(2/3)=4 17/27
Titik beloknya (2/3,4 17/27)
Langkah 2
Gambarkan titik-titik yang diperoleh pada langkah 1 pada koordinat kartesius. Titik-titik tersebut adalah sebagai berikut.
(0,9), (-1,0), (1,5;0), (-1/6,9 7/27), dan (2/3,4 17/27)
Langkah 3
Hubungkan titik-titik yang telah diletakan pada koordinat kartesius oleh kurva halus dengan memperhatikan naik-turun dan kecekungannya, sehingga diperoleh grafik sebagai berikut.