Materi Aplikasi Turunan
Mengutip buku Matematika terbitan Kementerian Pendidikan dan Kebudayaan Republik Indonesia, aplikasi turunan fungsi biasa digunakan untuk memecahkan permasalahan interval fungsi naik/turun, nilai maksimum atau minimum fungsi, serta kecepatan dan percepatan.
1. Menentukan Interval Fungsi Naik/Turun
Setiap gedung pastinya memiliki lift atau eskalator untuk memudahkan kita. Gerakan pada lift atau eskalator tersebut bisa kita gambarkan sebagai fungsi naik dan turun.
Gerakan eskalator atau lift dapat kita ilustrasikan seperti gambar grafik di bawah ini:
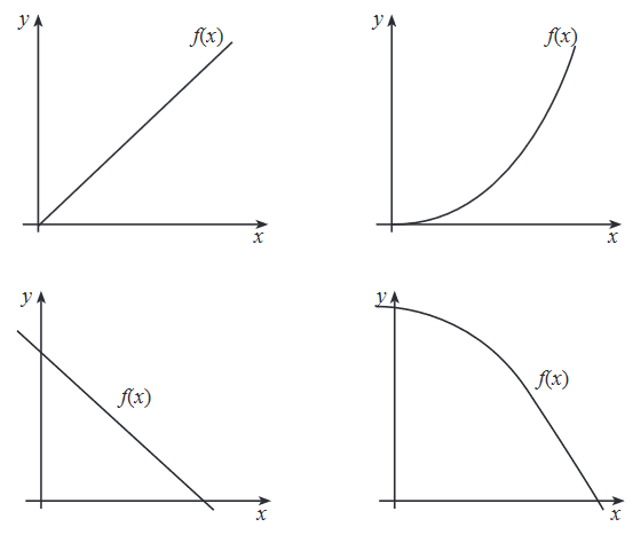

No comments:
Post a Comment