Aturan Rantai
Aturan rantai (chain rule) menyatakan bahwa turunan dari f(g(x)) adalah f′(g(x))⋅g′(x). Dengan kata lain, aturan rantai digunakan untuk mencari turunan komposisi dua fungsi atau lebih.
turan rantai memungkinkan kita untuk mencari turunan komposisi dua fungsi atau lebih. Komposisi fungsi yang biasanya diturunkan dengan aturan rantai adalah bentuk pangkat dari fungsi aljabar yang terdiri dari beberapa suku.
Sebagai contoh, bayangkan usaha untuk mencari turunan dari fungsi berikut:
Tanpa aturan rantai, pertama anda harus mengalikan bersama ke 60 faktor-faktor kuadrat dan kemudian mendiferensialkan atau menurunkan polinom (suku banyak) berderajat 120 yang dihasilkan.
Tentu saja kita tidak perlu melakukan itu, karena terdapat cara yang lebih baik. Setelah anda mempelajari aturan rantai ini, anda akan mampu menuliskan jawabannya dengan cepat berikut ini.
TEOREMA A: Aturan Rantai
Andaikan dan . Jika terdiferensialkan di dan terdiferensialkan di , maka fungsi komposit , didefinisikan oleh , terdiferensialkan di dan
Yakni,
atau dapat dituliskan juga sebagai
CONTOH 1:
Perhatikan kembali fungsi yang diperkenalkan pada bagian awal di atas. Carilah .
Penyelesaian:
Kita pikirkan ini sebagai

Fungsi yang luar adalah dan fungsi dalamnya adalah . Dengan demikian,



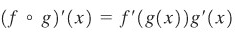

No comments:
Post a Comment